Enter a word or phrase in any language 👆
Language:
Translation and analysis of words by ChatGPT artificial intelligence
On this page you can get a detailed analysis of a word or phrase, produced by the best artificial intelligence technology to date:
- how the word is used
- frequency of use
- it is used more often in oral or written speech
- word translation options
- usage examples (several phrases with translation)
- etymology
линейная мера - translation to french
МЕРА МНОЖЕСТВА
Линейная мера; Плоская мера; Цилиндрическая мера; Альфа-мера Хаусдорфа; Хаусдорфова мера
линейная мера
mesure de longueur
мера
СТРАНИЦА ЗНАЧЕНИЙ В ПРОЕКТЕ ВИКИМЕДИА
Мера вероятности; Мера (река)
ж. в разн. знач.
mesure
меры длины - mesures de longueur
меры поверхности - mesures de surface
меры веса - mesures de poids
меры жидких тел - mesures de capacité
чувство меры - sens de la mesure
принять меры - prendre des mesures ( или des dispositions)
не знать меры - combler la mesure
в значительной мере - dans une grande mesure, à un fort degré
в известной мере - à un certain degré, dans une certaine mesure
временная мера - mesure temporaire
высшая мера наказания - peine capitale
в меру - convenablement ( при прил. ); suffisamment ( достаточно ); avec mesure ( не чересчур )
в меру чего-либо - dans la mesure de qch
не в меру - outre mesure; immodérément, à l'excès
ни в какой мере - aucunement, d'aucune façon
по крайней мере, по меньшей мере - au moins; pour le moins
по мере возможности - autant que possible, dans la mesure du possible
по мере моих (твоих и т. п. ) сил - dans la mesure de mes (tes, etc. ) forces
по мере того, как..., по мере (+ отглаг. сущ. ) - à mesure que, au fur et à mesure que...
сверх меры, без меры - outre mesure
mesure
меры длины - mesures de longueur
меры поверхности - mesures de surface
меры веса - mesures de poids
меры жидких тел - mesures de capacité
чувство меры - sens de la mesure
принять меры - prendre des mesures ( или des dispositions)
не знать меры - combler la mesure
в значительной мере - dans une grande mesure, à un fort degré
в известной мере - à un certain degré, dans une certaine mesure
временная мера - mesure temporaire
высшая мера наказания - peine capitale
в меру - convenablement ( при прил. ); suffisamment ( достаточно ); avec mesure ( не чересчур )
в меру чего-либо - dans la mesure de qch
не в меру - outre mesure; immodérément, à l'excès
ни в какой мере - aucunement, d'aucune façon
по крайней мере, по меньшей мере - au moins; pour le moins
по мере возможности - autant que possible, dans la mesure du possible
по мере моих (твоих и т. п. ) сил - dans la mesure de mes (tes, etc. ) forces
по мере того, как..., по мере (+ отглаг. сущ. ) - à mesure que, au fur et à mesure que...
сверх меры, без меры - outre mesure
mesure linéaire
линейная мера
Definition
Мера множества
математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (Δ) любого квадрата Δ полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов Δ1, Δ2,..., Δn,...; нижнюю грань чисел
взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m*(А) множества А. Нижняя (внутренняя) мера m* (А) множества А определяется как разность
где Δ - какой-либо квадрат, содержащий множество А, и 
- множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)Δ ́≥ ́0; 2) мера суммы
конечной или счётной системы попарно непересекающихся множеств A1, A2..., An... равна сумме их мер:
3) при перемещении множества как твёрдого тела его мера не меняется.
Своеобразие понятия "М. м." можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А, так и точки множества В; в то же время они резко различаются по мере: m (А) = 0, а m (В) = 1.
Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (См. Борель) (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.
Развитие ряда отделов современной математики привело к дальнейшим обобщениям - созданию т. н. абстрактной теории меры. При этом М. м. определяют аксиоматически. Пусть U - произвольное множество и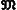 
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в 
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в , сумма А которых входит в , имеет место равенство
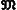- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в , сумма А которых входит в , имеет место равенство и если, кроме того, система удовлетворяет определённым дополнительным условиям. Множества, входящие в , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
удовлетворяет определённым дополнительным условиям. Множества, входящие в , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования. Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. - Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.
Ю. В. Прохоров.
Wikipedia
Мера Хаусдорфа
Мера Хаусдорфа — собирательное название класса мер, определённых на борелевской -алгебре метрического пространства . Построены Феликсом Хаусдорфом.
